Unit 1: Operations with Rational Numbers
Unit 1: This unit builds upon the student's understanding of rational numbers that was developed in 6th grade. In Grade 7, learning now moves to explore and ultimately formalizing rules for operations (addition, subtraction, multiplication, and division) with integers. Using both contextual and numerical problems, students should explore what happens when negative numbers and positive numbers are combined. Repeated opportunities over time will allow students to compare the results of adding, subtracting, multiplying, and dividing pairs of numbers, leading to the generalization of the rules. Fractional rational numbers and whole numbers should be used in computations and explorations. Students will be able to give contextual examples of integer operations, write and solve equations for real-world problems and explain how the properties of operations apply. Real-world situations could include profit/loss, money, weight, sea level, debit/credit, football yardage, etc.
_______________________________________________________________________________________________________________________________
NUMERICAL REASONING - integers, percents, fractions, decimal numbers.
7.NR.1 Solve relevant, mathematical problems, including multi-step problems, involving the four operations with rational numbers and quantities in any form (integers, percentages, fractions, and decimal numbers).
Video on Negative Numbers called Integers
Adding and Subtracting Integers
Multiplying and Dividing Integers
Review Integers
Video on Absolute Values
GAMES: Reviewing Integers
PRACTICE: Adding and Subtracting Integers
Multiplying and Dividing Integers
Modeling with Algebra Tiles
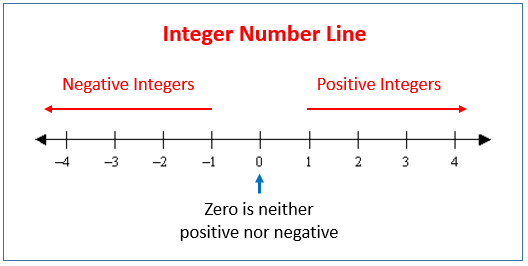
Integers - An integer is a whole number that can be positive, negative, or zero.
Example of integers are: -5, 1, 5, 8, 97, and 3,043.
Examples of numbers that are not integers are: -1.43, 1 3/4, and 3.14.